Segundo Desafio

Uma bala é atirada de um canhão e descreve uma parábola de equação y = -9x² + 90x. Determine a altura máxima atingida pela bala do canhão, sabendo que y é a altura em metros e x é o alcance, também em metros.

Para ajudar na resolução deste problema: Utilize a noção de coordenadas no vértice:
Seja uma função quadrática, Xv = -b/2a e Yv = f(Xv).

Solução:

A = -9 B= 90 C= 0

Delta= b² - 4.a.c
Delta= 90² - 4.(-9).0
Delta = 8100
__________________________________________________________________

Yv = -8100 / 4.(-9)
Yv = 225m

Aluno : Caique Lima
Turma: 1002

Zero da Função Quadrática (Raiz)

A parábola da função intercepta o eixo das abscissas em dois pontos. Estes pontos são denominados raiz da função ou zero da função.

Uma função quadrática possui de zero a duas raízes reais distintas.

Sendo  a função, para encontramos as suas raízes basta igualarmos y a 0 e solucionarmos a equação do segundo grau obtida:

Estes são os valores de x que levam a y = 0, estes valores são portanto as raízes desta função.

Exercícios de Função Quadrática

Treinem alguns exercícios de Função Quadrática publicadas pela aluna Luana de Oliveira (Turma 1002)

1) Escreva os coeficientes das funções abaixo:

a) f(x)= x² -7x +8

b)f(x)= x² +10x -5

c)f(x)= x² +15x -9

2) Encontre os zeros das funções abaixo:

a) f(x)= x² -6x +5

b)f(x)= x² -5x +2

c)f(x)= x² +4x -4

d)f(x)= x² +2x -1

3) Dada a função f(x)= x² +14x -15 calcule:

a)f(2)

b)f(1)

c)f(0)

d)f(5)

4) Resolva a equação que está faltando o coeficiente b :

x² -8 = 0

5) Resolva a equação que está faltando o coeficiente c:

x² - 15x = 0

FUNÇÃO QUADRÁTICA

Uma função quadrática é uma função polinomial da forma:

se, e somente se a ≠ 0. O gráfico de uma função quadrática é uma parábola cujo maior eixo é paralelo ao eixo y, se tal função for contínua. A expressão:

na definição de uma função quadrática é um polinômio de segundo grau ou um polinômio de grau 2, porque o maior expoente de  é 2.

Se a função quadrática é igualada a zero, o resultado é uma equação quadrática. As soluções para a equação são chamadas raízes da equação ou os zeros da função, e são os interceptos do gráfico da função com o eixo x.

  f(x) = x² - x - 2 

Raízes :

 As raízes da função quadrática são os valores de x cuja imagem é 0, ou seja, em que o gráfico corta o "eixo x". O número de raízes depende do valor do discriminante, geralmente denotado pela letra grega delta, definido por:

Para:

•  a função terá duas raízes.
•  a equação terá uma raiz apenas (com maior precisão, diz-se que a equação tem duas raízes iguais)
•  não terá raíz (com maior precisão, diz-se que a equação não tem raízes reais, tendo duas raízes complexos conjugados).

As duas raízes da equação quadrática  onde  são

Essa fórmula é chamada de Fórmula Quadrática.

• Dado 
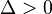• Se , então existem duas raízes distintas uma vez que  é um número real positivo.
• Se  então as duas raízes são iguais, uma vez que  é igual a zero.
• Se  então as duas raízes são números complexos conjugados, uma vez que  é imaginário. Efetuando  e  ou vice versa, é possível fatorar  como   

( enviado por : Eduarda da Costa Araujo turma : 1001 )

 

Trigonometria

Trigonometria (do grego trigōnon "triângulo" + metron "medida") é um ramo da matemática que estuda as relações entre os comprimentos de 2 lados de um triângulo retângulo (triângulo onde um dos ângulos mede 90 graus), para diferentes valores de um dos seus ângulos agudos. A abordagem da trigonometria penetra outros campos da geometria, como o estudo de esferas usando a trigonometria esférica.
A trigonometria tem aplicações importantes em vários ramos, tanto como na matemática pura, quanto na matemática aplicada e, consequentemente, nas ciências naturais. A trigonometria é comumente ensinada no Ensino Médio.

Aplicações da trigonometria

Existem diversas aplicações da trigonometria e das funções trigonométricas. Por exemplo, a técnica da triangulação é usada em astronomia para estimar a distância das estrelas próximas; em geografia para estimar distâncias entre divisas e em sistemas de navegação por satélite. As funções seno e cosseno são fundamentais para a teoria das funções periódicas, as quais descrevem as ondas sonoras e luminosas.

Campos que fazem uso da trigonometria ou funções trigonométricas incluem astronomia (especialmente para localização de posições aparentes de objetos celestes, em qual a trigonometria esférica é essencial) e portanto navegação (nos oceanos, em aviões, e no espaço), teoria musical, acústica, óptica, análise de mercado, eletrônica, teoria da probabilidade, estatística, biologia, equipamentos médicos (por exemplo, Tomografia Computadorizada e Ultrassom), farmácia, química, teoria dos números (e portanto criptologia), sismologia, meteorologia, oceanografia, muitas das ciências físicas, solos (inspeção e geodesia), arquitetura, fonética, economia, engenharia, gráficos computadorizados, cartografia, cristalografia e desenvolvimento de jogos.

Por: Cleyton da Silva Batista
Turma: 1001
C.E. São Bernardo

Para Quebrar a Cabeça

Para distrair coloquei um desafio para vocês. Daqui há quinze dias eu verei se alguém mandou a resposta. Quem conseguir ganha um prêmio. Abraços

http://rachacuca.com.br/teste-de-einstein/

Primeiro Desafio

1º DESAFIO

(ENEM 2000) Um boato tem um público alvo e alastra-se com determinada rapidez. Em geral, essa rapidez é diretamente proporcional ao número de pessoas desse público que conhece o boato e diretamente proporcional também ao número de pessoas que não o conhece. Em outras palavras, sendo R a rapidez e propagação, P o público-alvo e x o número de pessoas que conhece o boato, tem-se: R(x) = kx (P – x), em que k é uma constante positiva característica do boato. Considerando o modelo acima descrito, se o público-alvo é de 44000 pessoas, então a máxima rapidez de propagação ocorrerá quando o boato for conhecido por um número de pessoas?

Solução enviada por Cleyton da Turma 1001

R(x) = kx (P – x) 
R(x) = kx (44000 – x) 
R(x) = 44000kx – kx² 
R(x) = – kx² + 44000kx 
xv = -b/2a => xv = -44000k/-2k, corta k com k e então fica 
xv = 44000/2 => xv = 22000 
resposta 22000 
Obs. Trata-se de uma função quadrática que tem a boca voltada para baixo, ou seja, admite máximo. Esse máximo é atingido quando x = 22000, que é a resposta do problema.

PARA DIVULGAR

Meus alunos das turmas 1001 e 1002 do Colégio Estadual São Bernardo. Este blog é de vocês. Quero que vocês pesquisem, coloquem vídeos, fotos, matérias sobre o estudo da Matemática. O foco principal é FUNÇÃO QUADRÁTICA  e TRIGONOMETRIA. Mas podem abordar outros assuntos, sem problema. No dia 01 de outubro, eu divulgarei a pontuação sobre o uso do blog, Valor total = 3,0 pontos. Aproveitem! Não pensem na pontuação, mas na criatividade que cada um tem.

ALGUMAS APLICAÇÕES DA FUNÇÃO QUADRÁTICA

Dentre as aplicações encontradas, as mais relevantes foram: lançamento de projéteis, controle de processos (projetos de reatores), faróis de automóveis, , antenas parabólicas e radares, na geometria e nos esportes.

Análise e Controle de Processos: Segundo informações de profissionais da área de engenharia um reator é um equipamento utilizado para produzir reações químicas. Um exemplo muito prático é a panela de pressão no sentido de que propicia reações químicas entre os alimentos nela contidos. Outro exemplo são os reatores do Polo Petroquímico que produzem a matéria-prima para algumas empresas, como de plásticos ou de tintas. Neste sentido, para manter a temperatura de um reator constante, modela-se a situação com uma função quadrática expressa da seguinte forma:  Equação da função de Transferência onde kc é uma constante do processo, obtida através da construção de gráficos experimentais.

Lançamento de Projéteis: Quando se lança um objeto no espaço (pedra, tiro de canhão,...) visando alcançar a maior distância possível, tanto na horizontal como na vertical, a curva descrita pelo objeto é aproximadamente uma parábola, se considerarmos que a resistência do ar não existe ou é pequena. O lançamento de projéteis é modelado por uma função quadrática porque é um movimento acelerado pela ação do campo gravitacional.

PEQUENO TEXTO

Há uma grande divergência ao enquadrar a Matemática com Ciência Exata ou Ciência Humana. Acredito que com sua grandeza e complexidade pode ser enquadrada nas duas ciências. Este blog foi idealizado para auxílio no desenvolvimento dos alunos no estudo desta grande ciência - A Matemática.

INÍCIO DO BLOG

Estou iniciando um blog para colocar as atividades para o primeiro ano do Colégio Estadual São Bernardo. Aos poucos colocarei mensagens que auxiliem no estudo da Matemática