Coordenada do Vértice

Coordenadas do vértice da parábola

   Quando a > 0, a parábola tem concavidade voltada para cima e um ponto de mínimo V; quando a < 0, a parábola tem concavidade voltada para baixo e um ponto de máximo V. 

Em qualquer caso, as coordenadas de V são . Veja os gráficos:

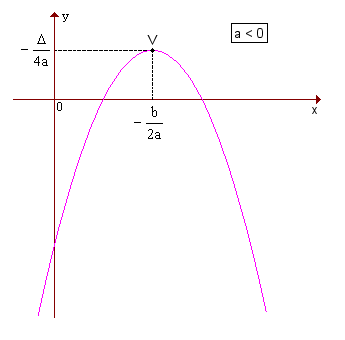
Imagem

     O conjunto-imagem Im da função y = ax² + bx + c,  a 0, é o conjunto dos valores que y pode assumir. Há duas possibilidades:

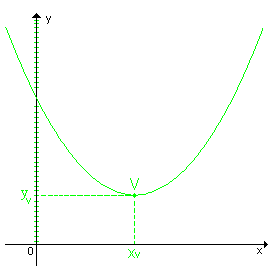
1ª - quando a > 0,

a > 0

2ª quando a < 0,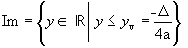                                                     

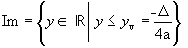
a < 0

Construção da Parábola

   É possível construir o gráfico de uma função do 2º grau sem montar a tabela de pares (x, y), mas seguindo apenas o roteiro de observação seguinte:

1. O valor do coeficiente a define a concavidade da parábola;
2. Os zeros definem os pontos em que a parábola intercepta o eixo dos x;
3. O vértice V  indica o ponto de mínimo (se a > 0), ou máximo (se a< 0);
4. A reta que passa por V e é paralela ao eixo dos  y é o eixo de simetria da parábola;
5. Para x = 0 , temos y = a · 0² + b · 0 + c = c; então  (0, c) é o ponto em que a parábola corta o eixo dos y.

Sinal

   Consideramos uma função quadrática y = f(x) = ax² + bx + c e determinemos os valores de x para os quais y é negativo e os valores de x para os quais y é positivos.
    Conforme o sinal do discriminante  = b² - 4ac, podemos ocorrer os seguintes casos:

1º -   > 0
   Nesse caso a função quadrática admite dois zeros reais distintos (x1  x2). a parábola intercepta o eixo Ox em dois pontos e o sinal da função é  o indicado nos gráficos abaixo:

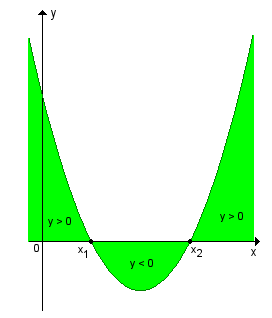
quando a > 0

y > 0 (x < x₁ ou x > x₂)
y < 0 x₁ < x < x₂

quando a < 0

y > 0 x₁ < x < x₂

y < 0  (x < x₁ ou x > x₂)

Publicado por Eduarda Costa (1001)