Professor Rodrigo Sacramento - A Curtição do Sacra (Função Quadrática) N...

CANÇÃO DA TRIGONOMETRIA Aula de Matemática com Música

Desafio da Semana

Um fazendeiro tem 100 m de cerca para construir uma área retangular. Determine suas dimensões sabendo que a sua área equivale a 600 metros quadrados:

Dica: Chame as dimensões do retângulo de x e y:

Como área do retângulo é base x altura então: A = xy = 600.

Resposta por Luana de Oliveira

y= 50-x
x(50-x)= 600
-x²+50x-600=0
Delta: b²-4ac
50²-4.(-1).(-600)
2500-2400= 100

x= -50+- 10/ -2
-50+10/-2=20
-50-10/-2=30

x= 20 y=30

Problema Resolvido de Função Quadrática

PM ES 2013 – Exatus)

Uma agência de viagens vende pacote turísticos coletivos com destino a Fortaleza. Um pacote para 40 clientes custa R$ 2000,00 por pessoa e, em caso de desistência, cada pessoa que permanecer no grupo deve pagar mais R$ 100,00 por cada desistente do pacote de viagem. Dessa forma, para que essa agência obtenha lucro máximo na venda desse pacote de viagens, o número de pessoas que devem realizar a viagem é igual a:

Solução: O preço total é dado pela quantidade de pessoas vezes o preço por pessoa, que é 2000 mais 100 por desistente. C(x) = x(2000 + 100(40 – x))

C(x) = x(2000 + 4000 – 100x)                   C(x) = x(6000 – 100x)
C(x) = 6000x – 100x²
Temos uma função do segundo grau.
Vamos calcular as raízes: 6000x – 100x² = 0.           60x – x² = 0
X(60 – x) = 0         Assim, x = 0 ou x = 60

Como em nossa função o valor de a = -100 < 0, o gráfico é uma parábola para baixo, portanto possui valor máximo, e é exatamente o valor entre as raízes 0 e 60, portanto o valor máximo ocorre quando x = 30.

Bhaskara

A Índia foi berço de nascimento de um dos maiores matemáticos do mundo, Bhaskara.

 ... nasci na cidade de Ujein, às margens do rio local, de uma mulher que possuía uma boa saúde, mas, por infelicidade e complicação de parto, morreu ao me dar à luz em 1114. Meu pai era um alto funcionário do marajá local, e isso permitiu que eu tivesse oportunidade de me instruir nas ciências e nas leis.
Com a morte de seu pai, em 1134, Bhaskara assumiu o cargo de secretário do governo de Ujein, espécie de juiz especializado em inventários:

"...foi então que Brabmagta me convidou para ser o matemático do governo. Trabalhava particularmente com problemas de quadrado, os quais se relacionavam às partilhas dos inventários. Di­vertia-me resolvendo aqueles exercícios, que para muitos eram com­plicados, mas com minha técnica de solução...

O  que Bhaskara chama de problemas de quadrado refere-se hoje as equações do segundo grau.

... o quadrado da quantidade de ouro referente ao primeiro Órfão mais três vezes essa mesma quantidade doada ao seguinte órfão deverá ser igual, por Justiça, a trinta e oito gramas...
Bhaskara imortalizou-se aos 25 anos quando escreveu seu célebre Lilavati Vijaganita Grahagonita Gola, cujas palavras traduzidas individualmente, são: bonita cálculo - planetas - esfera. Aparentemente o manuscrito que teria sido escrito por Bhaskara e achado em Cachemira no século passado era dividido em quatro capítulos: Poesia, Matemática, Astronomia e Geometria. Daí o título confuso. É interessante notar que o trabalho desse matemático é todo escrito em versos destinados a sua filha:
"...minha filha, minha filha, a coisa mais bonita da Índia, me fale de suas dúvidas. Oh, querida, você esteve a tarde contando macacos, uns estavam nas arvores, outros no alto da montanha­.....
O Lilavati Vijaganita traz ao público inúmeras descobertas de seu autor, sendo a mais célebre a fórmula que resolve as equações do segundo grau, seguida da clássica regra de três que Bhaskara chamou regra de quatro (três valores conhecidos e um desconhecido). Aparece também o valor de p como sendo 3, 14, resquícios da trigonometria de Ptolomeu e o Teorema de Pitágoras
minha filha Lilavati tem me questionado sobre os valores do lado oposto e adjacente de um triângulo retângulo.
Os gregos nos ensinaram a responder sobre o seno e o co-seno de um ângulo...
Nesse trecho do Lilavati víjaganita o autor chama sua filha de Lilavati, o que tem induzido muitos escritores a pensar que a melhor tradução do titulo de seu livro seja Matemática de Lilavati.
Sobre a filha de Bhaskara, existem duas versões nos textos antigos do século
XIII registrados pelos padres do mosteiro de Constantinopla:
"...quando os bárbaros invadiram a cidade de Uzein, seqüestraram todas as pessoas importantes, bem como seus bens. Lilavati tinha apenas treze anos. Seu pai, questionado pelos invasores sobre sua fórmula de re­solver problemas, recusou-se a falar. Dizia tê-la esquecido já há muitos anos. Para ajuda-lo com a memória, levaram sua filha pa­ra o alto de uma torre, despiram-na e amarraram -lhe as pernas, abertas. Solta, ela deslizou sobre os bambus que conduziam a uma lâmina afiada que dividiu seu corpo em duas  partes...
 .... Bhaskara prometeu a Lilavati um horóscopo que identificasse o dia e hora ideal que deveria se casar. Uma vez determinado o momento, Lilavati esperou dois anos para desposar um jovem hindu. Quando faltavam alguns minutos para a cerimônia ao casamento, a jovem perdeu uma pérola que tinha pertencido à sua mãe e, entretida em procura-la, esqueceu do casamento. Bhaskara então recusou-se a  casá-la e Lilavati cometeu suicídio...
A obra deste hindu traz, além de informações matemáticas, um raio X da sociedade de sua época. Relata que uma escrava alcançava preço máximo de quinze para dezesseis anos. Caso fosse bonita e virgem, valia oito bois; bonita e não virgem, quatro; feia e virgem, seis; e feia e não virgem, dois bois. Os juros praticados em seu tempo eram de quatro por cento ao mês, e o prazo de pagamento dos empréstimos não ultrapassava cinco meses. As dívidas não honradas davam ao credor o direito de escravizar a mulher e filhos do devedor, o qual, porém, não sofria nenhuma punição. Bhaskara teria escrito.
Esses homens que pedem clemência, quando da execução judicial, não entendem nossas leis. Por que emprestam dinheiro e arrendam terras se sabem que não poderão cumprir com as dívidas contraídas? Minha função é julgar e partilhar como prescreve nosso livro maior (espécie de Constituição)...
Em 1185, Bhaskara, então com 71 anos, morreu afogado num rio onde teria ido nadar.

Origem da Função Quadrática

Há registros de problemas envolvendo equações quadráticas com três termos, deixados pelos babilônios há aproximadamente 4000 anos .Esses estudos demonstram uma grande flexibilidade existente na Algébra desenvolvida entre eles , outros povos também contribuíram com esta parte da Álgebra até que se chegasse à representação atual de uma equação quadrática ax² + bx + c = 0com a não nulo , na qual o valor de x é obtido pela fórmula de Bháskara.
Essa organização de simbolos , que simplifica o estudo das quadráticas , é recente se for comparada com a idade da Álgebra.Foi no século XVII que Descartes utilizou as letras a, b e c para representar quantidades conhecidas e as letras do final do alfabeto , x, y e z , para representar as incógnitas. Além disso passou a usar a representação x² em lugar de x . x e x³ em lugar de x . x . x - René Descartes (1596-1650) era francês , formado em Direito e aos vinte anos sua insatisfação lançou-o como reformulador da filosofia que influenciava os acadêmicos da época. O seu mais celébre tratado, O discurso sobre o método para raciocinar bem e procurar a verdade nas ciências , é de 1637 e originou a Geometria Cartesiana , hoje dita Geometria Analítica , que nos mostra como as cinco operação aritméticas correspondem a construções feitas com régua e compasso,justificando a introdução de termos aritméticos em geometria.

Texto: Cleyton da Silva (1001)

Quarto Desafio

Vamos ao quarto desafio deste blog:
Só vale quem acertar por exato os dois problemas abaixo: Quem puder comprovar com cálculos seria melhor e até para questões de desempate. Mas você pode colocar aqui ou no grupo Se Liga 1001 ou Se Liga 1002 no Facebook.
Queria pedir aos alunos que visualizam mas não conseguem participar que mande para meu e-mail prof.marcelo@gmail.com ou sinalize no grupo mencionado acima. O importante é participar.

(1) Sabendo que certo ângulo de lançamento, a altura K lançada por uma pedra, em metros, em função do tempo t, em segundos é dada por K = (-1/60) t² + t. A partir disso, resolva:

(a) Em quanto tempo, após o lançamento da pedra ela atinge a altura máxima?

Xv = -1/2(-1/60) = 1/1/30 = 30 segundos.

(b) Qual a altura máxima atingida pela pedra em relação ao plano horizontal de onde foi lançada?

Yv = (-1/60). (900) + 30 = -15 + 30 = 15 metros.

(2) Segundo afirmam os fisiologistas, o número N de batimentos cardíacos por minuto de um indivíduo sadio e, em repouso varia em relação a temperatura ambiente (T) em graus Celsius e é dada pela função N(T) = (0,5)T² - 4T + 90.

(a) Se uma pessoa estiver dormindo num quarto cuja refrigeração seja 20º C. Qual será o número de batimentos cardíacos por minuto dessa pessoa?

N(20) = (0,5) (400) - 4(20) + 90 = 200 - 80 + 90 = 170 batimentos cardíacos.

^(b) A que temperatura, o número de batimentos cardíacos por minuto de uma pessoa sadia e, em repouso atingirá 90?

90 = (0,5) T.T - 4T + 90
90 - 90 = 0,5TT - 4T
0,5TT - 4T = 0
T(0,5T - 4) = 0,
T = 0 e 0,5T - 4 = 0
0,5T = 4
T = 4/0,5
T = 8º C

História da Matemática

A história da matemática é uma área de estudo dedicada à investigação sobre a origem das descobertas da matemática e, em uma menor extensão, à investigação dos métodos matemáticos e aos registros ou notações matemáticas do passado.

Anteriormente à modernidade e à expansão mundial do conhecimento, os exemplos escritos de novos progressos matemáticos tornaram-se conhecidos em apenas poucas localidades. Os textos matemáticos mais arcaicos disponíveis que nos são conhecidos são o Plimpton 322 (matemática babilônica, cerca de 1900 a.C.) , o Papiro Matemático de Rhind (matemática egípcia, cerca de 2000-1800 a.C.) e o Papiro Matemático de Moscou (matemática egípcia, cerca de 1890 a.C.). Todos estes textos versam sobre o então chamado Teorema de Pitágoras, que parece ser o progresso matemático mais amplamente difundido depois da aritmética básica e da geometria.

A contribuição greco-helênica refinou grandiosamente os métodos (especialmente através da introdução do raciocínio dedutivo e do rigor matemático em provas) e expandiu o tema da matemática, isto é, aquilo de que ela trata. O estudo da matemática como um tópico em si mesmo começa no século VI a.C. com os pitagóricos, os quais cunharam o termo "matemática" a partir do termo μάθημα (mathema) do grego antigo, significando, então, "tema do esclarecimento". A matemática chinesa fez contribuições já muito cedo, incluindo o sistema de notação posicional . O sistema númerico indo-arábico e as regras para o uso de suas operações, atualmente em uso no mundo todo, foi provavelmente desenvolvido em torno do ano 1000 d.C. na Índia e transmitido ao Ocidente através da matemática islâmica . A matemática islâmica, por sua vez, desenvolveu e expandiu a matemática conhecida destas civilizações9 . Muitos textos gregos e árabes sobre matemática foram então traduzidos ao latim, o que contribuiu com o desenvolvimento da matemática na Europa medieval.

Dos tempos antigos à Idade Média, a eclosão da criatividade matemática foi frequentemente seguida por séculos de estagnação. Começando no Renascimento, no século XVI, novos progressos da matemática, interagindo com as novas descobertas científicas, foram realizados de forma crescente, continuando assim até os dias de hoje.
Publicado por Caique (Turma 1002)

Origem: wikipedia

Coordenada do Vértice

Coordenadas do vértice da parábola

   Quando a > 0, a parábola tem concavidade voltada para cima e um ponto de mínimo V; quando a < 0, a parábola tem concavidade voltada para baixo e um ponto de máximo V. 

Em qualquer caso, as coordenadas de V são . Veja os gráficos:

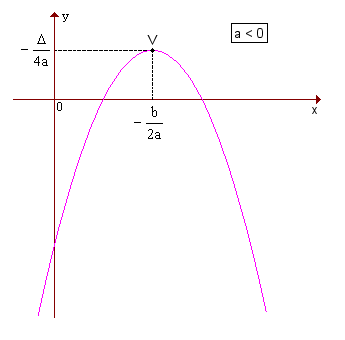
Imagem

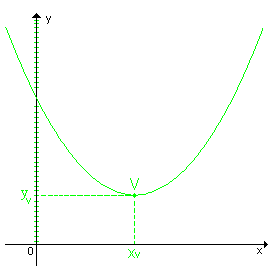
     O conjunto-imagem Im da função y = ax² + bx + c,  a 0, é o conjunto dos valores que y pode assumir. Há duas possibilidades:

1ª - quando a > 0,

a > 0

2ª quando a < 0,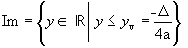                                                     

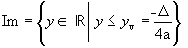
a < 0

Construção da Parábola

   É possível construir o gráfico de uma função do 2º grau sem montar a tabela de pares (x, y), mas seguindo apenas o roteiro de observação seguinte:

1. O valor do coeficiente a define a concavidade da parábola;
2. Os zeros definem os pontos em que a parábola intercepta o eixo dos x;
3. O vértice V  indica o ponto de mínimo (se a > 0), ou máximo (se a< 0);
4. A reta que passa por V e é paralela ao eixo dos  y é o eixo de simetria da parábola;
5. Para x = 0 , temos y = a · 0² + b · 0 + c = c; então  (0, c) é o ponto em que a parábola corta o eixo dos y.

Sinal

   Consideramos uma função quadrática y = f(x) = ax² + bx + c e determinemos os valores de x para os quais y é negativo e os valores de x para os quais y é positivos.
    Conforme o sinal do discriminante  = b² - 4ac, podemos ocorrer os seguintes casos:

1º -   > 0
   Nesse caso a função quadrática admite dois zeros reais distintos (x1  x2). a parábola intercepta o eixo Ox em dois pontos e o sinal da função é  o indicado nos gráficos abaixo:

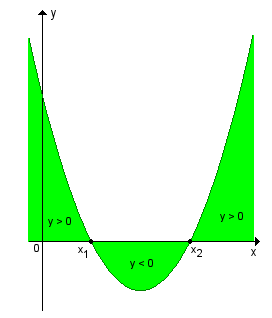
quando a > 0

y > 0 (x < x₁ ou x > x₂)
y < 0 x₁ < x < x₂

quando a < 0

y > 0 x₁ < x < x₂

y < 0  (x < x₁ ou x > x₂)

Publicado por Eduarda Costa (1001)

Música da Função Quadrática

Paródia da música ''Dark Horse'' da Katy Perry no Youtube, ai nesse vídeo fala da Função Quadrática https://www.youtube.com/watch?v=AD5tHGyUmjw não sei se é boa pra por no blog, mas dá uma olhada e vê se ta legal 

Aluna : Eduarda  

Turma : 1001

Área de anexos

Visualizar o vídeo Paródia da música "Dark Horse": Função Quadrática. UNASP EC do YouTube

Paródia da música "Dark Horse": Função Quadrática. UNASP EC

Aplicação na Função Quadrática

Existem objetos de aprendizagem que contribuem muito para que os alunos aprendam a relacionar variáveis (as letras) em uma função, realizar experimentos, alterar valores e verificar relações de causa e efeito. Eis o objeto recomendado para a atividade usando computadores na escola:

Clique no link para abrir o simulador: projectile-motion.

No simulador, os alunos podem modificar a massa e diâmetro dos projéteis, sua velocidade inicial, o ângulo de lançamento e até mesmo o efeito da resistência do ar. Além disso, é possível brincar de atingir o alvo marcado no chão. Para tirar o máximo de proveito dessa atividade o professor deve realizar perguntas aos alunos no que diz respeito às alterações nas variáveis, como por exemplo pedir que eles variem apenas a massa do projétil e que observem o que acontece com o tempo e a distância. É importante estimular os alunos a estabelecerem e anotarem as relações percebidas e por fim, desafiá-los com relação a função quadrática que relaciona a distância do lançamento com o quadrado da variável tempo.

Produzindo Gráficos com uma Planilha Eletrônica (Microsoft Office ou BrOffice)

Acesse o post Estudo de funções matemáticas usando o Excel [Função Quadrática]  e aprenda de forma fácil e rápida como construir gráficos de funções do 2º grau e outros tipos de funções. Neste link a versão para o LibreOffice.

O alunos podem trabalhar no seu próprio gráfico da função quadrática utilizando uma planilha eletrônica como o software livre BrOffice: http://www.broffice.org/

O primeiro passo é criar uma pequena tabela de valores de x e y. Na coluna dos valores de x, basta digitar alguns valores que formarão os pontos do gráfico e permitirão a construção da curva.

Na coluna de valores de y, digitamos uma função quadrática na célula correspondente ao menor valor de x. Como exemplo, usaremos a função y = x² - 8x + 12. Observe a imagem abaixo.

Observe que a função y = x² - 8x + 12 é escrita na célula A2 da seguinte forma: =POTÊNCIA(A2;2)-8*A2+12 . A2 corresponde ao valor de x e, entre parênteses é acompanhado do número 2, indicando que o valor do x é elevado ao quadrado. POTÊNCIA é uma função matemática disponível no programa. Clicando no ponto preto em B2 e arrastando até a célula B6, os cálculos são feitos automaticamente.

Para gerar o gráfico, basta selecionar as colunas e clicar no ícone de construção de gráficos (semelhante ao gráfico tipo pizza) e selecionar as opções apresentadas na imagem acima. Feito isso, o gráfico deve aparecer após clicar no botão Concluir.

Eu sugiro deixar os alunos experimentarem outros valores, além de alterarem formatos e caracterísiticas do gráficos, de forma a que eles possam relacionar a variáveis envolvidas, permitindo que a experimentação contribua para a aprendizagem dos conceitos. Essa é uma boa oportunidade para apresentar aos alunos as raízes da função ( ou zeros de uma função), valores de x que resultam em y = 0. Também pode-se solicitar aos alunos para tornarem negativo o valor de x ao quadrado na função e verificarem o que acontece com o vértice da parábola.

Nas atividades de sala de aula, seria importante trabalhar a construção do gráfico da função utilizando calculadoras e papel quadriculado (milimetrado) e  após recriar os mesmos gráficos usando os computadores da escola.

Uma atividade interessante que pode envolver os alunos na produção da avaliação é pedir que eles criem funções quadráticas como desafios e troquem com os colegas para a produção no computador. Os pares ou pequenos grupos poderiam apresentar e discutir seus resultados em conjunto e isso permitiria a avaliação do aproveitamento dos alunos, além dos esclarecimentos necessários às dificuldades encontradas.

Terceiro Desafio

Com base na aula do dia 04 de agosto de 2014. Resolva os problemas coloque as respostas aqui ou no face, Mas me avisem porque desta vez vale um presente especial para o primeiro que acertar as duas questões abaixo:

(Questão 01)

O movimento de um projétil, lançado para cima verticalmente, é descrito por: y = – 40x² + 200x. Onde y é a altura, em metros, atingida pelo projétil x segundos após o lançamento. 

(a) Qual o tempo que esse projétil permanece no ar?

(b) Qual é altura máxima atingida pelo projétil?

Solução:

(a) Xv = -200/2.(-40)= -200/-80= 2,5 segundos.

(b) Yv = -40.(2.5)² + 200.(2,5)
-40.(6,25) + 500
- 250 + 500 = 250m

(Questão 02)

Em cada uma das funções abaixo encontre o vértice e classifique em ponto máximo ou mínimo a função dada:

.

(a) f(x) = x2 - 8x + 15 (b) f(x) = 3x² - 6x + 24 (c) f(x) = -5x² +10x - 20 Solução:  (a) Xv = 8/4 = 2     Yv =2.(2) - 8.(2) + 15 = 4 - 16 + 15 = 3. Vértice (2,3) Tem ponto minimo pois a concavidade é para cima (a > 0) (b) Xv = 6/2.(3) = 6/6 = 1  Yv = 3,(1)²-6.(1) + 24 = 3 - 6 + 24 = -3 + 24 = 21 Vertice (1,21) Tem ponto mínimo. (c) Xv = -10/2.(-5) = -10/-10 = 1   Yv = -5.(1) + 10.(1) - 20 = -5 + 10 - 20 = -15 Vértice (1,-15) Tem ponto Máximo pois a concavidade é para baixo (a < 0)  Colaboração na Resposta: CLEYTON DA SILVA (1001) LUANA DE OLIVEIRA (1002) GLEICE PAULINO (1002)